Motion Analysis, Structure from Moion

Geometric Analysis of SFM

The problems I have investigated are related to basic processes in the perception of three-dimensional motion, shape and their relationship. Many psychophysical experiments as well as computational considerations convincingly show that actual systems cannot estimate exact distances and shapes, but instead derive a distorted version of space. What I have been studying is the geometric distortion between perceptual space (computed space) and actual space, which is difficult to model due to the complexity of the scene (scene can change unpredictably, and the traditional approach to this problem is to adopt a statistical approach with a lot of assumptions). The geometrical approach of our work is helpful towards obtaining an intuitive grasp of this complex problem.

From these geometric studies, many ambiguities inherent in the structure from motion problem emerge. A clear understanding of these ambiguities is in turn crucial to the development of more robust algorithms. Our modeling of depth distortion also points to the rich synergistic relationship between motion estimation and depth estimation. While the traditional approach has been to remove depth from the equations so as to formulate an elegant algorithm, this elegance is obtained at the expense of stabilities of the recovery process. Our study points to the potential offered by simultaneous estimation of motion and depth.

I also attempt to understand from these results the space-time representation reconstructed inside our head. Since metric shape cannot be computed in practice, vision systems have to compute a number of alternative space and shape representations for a hierarchy of visual tasks, ranging from obstacle avoidance through homing to object recognition. My current research interests are concerned with understanding the large spectrum of these representations. One possible representation is that of the ordinal depth; the metric aspects are ignored but only the order of the depth points are represented. The advantage is that ordinal depth can be robustly recovered. The following figure shows the ordinal depth recovered, rendered in colour (cold colors represent near depths, warm colors represent far depths). Currently, I am working on using ordinal depth representation for tasks such as landmark-based navigation (see Robust scene recognition).

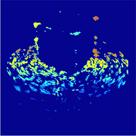
Fig 1. Left: Scene in view. Right: its ordinal depth reconstruction.

I have continued my work in motion analysis. One main thrust of my research now is in using sparse signal representation techniques to address the 3D motion segmentation problem, as well as change detection in video sequences with complications caused by complex and dynamic behavior such as ocean waves, waving trees, rain and moving clouds.

Motion Segmentation

Motion segmentation is a challenging problem in visual motion analysis. The idea is to segment the scene into multiple rigid-body motions, based on the point trajectories or optical flow observed in multiple camera views. It is a challenging problem because it requires the simultaneous estimation of an unknown number of motion models, without knowing which measurements correspond to which model. This problem can be cast as a subspace clustering problem in which point trajectories associated with each motion are to be clustered together. Recent works [Elhamifar & Vidal, 2012, Liu 2010, Rao et al., 2009] introduced compressed sensing techniques to subspace segmentation. We seek to extend these sparsity-based techniques as there are many difficulties with the current motion segmentation techniques. For instance, most current techniques cannot automatically estimate the number of motion clusters, and can only tolerate a small amount of missing entries and outliers. Our research include: 1) to better capture the global structures of data than current sparse techniques and to better estimate the number of motion clusters via the mixed norm approach; 2) to better handle the conditions where missing data, noise, and outliers are prevalent, and when the motions are partially dependent.

Compared to the recent LRR formulation proposed in [Liu 10], we wish to recover not only a low rank coefficient matrix Z, but also a coefficient matrix that has a particular sparsity pattern: the non-zero values appear in blocks, though not necessarily of the same length for each block. We propose minimizing a mixed L2/ L0 norm of the matrix Z comprising of two terms:

min. ||Z||_2,0 + ||Z||_0,2 + ||E||₀ s.t.  X = XZ + E     

This problem can be relaxed into the following version:

min. ||Z||_2,1 + ||Z||_1,2 + ||E||₁ s.t.  X = XZ + E

This mixed norm formulation encourages a common set of trajectories chosen for self expression, and thus facilitates the estimation of the number of motion groups. Due to the recent advances [Ding, Sun, Toh] in computing the Moreau-Yoshida regularizations of the mixed-norms in the above problem, we are excited by the possibility of being able to efficiently solve the model as well as demonstrating the model’s capability.

Change Detection

We assume that any variation in the background’s appearance (whether caused by intensity change, or non-stationary background) are highly constrained. Therefore a matrix composed of vectorized image frames can be approximated by a low-rank matrix, and the moving foreground objects can be detected as sparse outliers in this low-rank representation. In other words, a matrix composed of vectorized image frames D’ can be approximated as the sum of a low-rank matrix D representing the background with its highly redundant nature, and a sparse matrix E consisting of the moving objects treated as sparse outliers. We then seek to solve the following optimization problem:

min_D,E   rank(D) + λ ||E||₀

s.t.  D’ = D + E

where E is a sparse matrix with most of its entries being zero, and λ is an appropriate regularizing parameter.

The ability to handle target objects of different scales is also a perennial challenge in many segmentation problems and is also present in the preceding low-rank formulation (manifested by the regularizing parameter λ. The root of this problem lies in that the precise definition of the foreground target is intricately linked with the object of interest in the scene (i.e. one’s purpose) and can be well defined only if the object of interest or its salient characteristics is known to us. However, knowing about the object of interest even before segmenting the scene seems to make the problem as one of many chicken-egg problems in computer vision, as we usually need to segment the scene in order to recognize the objects in it. So, how can we identify an object and know its probable size even before segmenting it? Our proposed approach is to make a weak identification of the object of interest such as a rough region of interest. Obtaining these weak identifications without doing any segmentation is not a difficult problem as it can be done using low-level saliency cues in the visual attention systems.

Resolving the scale issue allows us to fully realize the potential of the RPCA method, without having to resort to smoothness prior such as MRF, thus allowing targets of various sizes to be delineated cleanly under various challenging conditions mentioned above. The significant improvement in the accuracy and the acuity of detection compared to the state-of-the-art techniques can be seen in the following results

o Non-stationary Background: this depicts a campus scene, with a large swaying tree and a person walking along the walkway. The magnitude of the tree motion is larger than that of the human. As can be seen from the results, the human silhouette is cleanly delineated in the foreground mask, which is typically not the case for many other methods that imposed smoothness prior on the foreground shape. In the background extracted, there is no ghostly presence resulting from residual human presence not cleanly removed. When viewed in video sequence, the effect is much clearer, and it can also be seen that the motion of the swaying tree is largely retained in the background.

Foreground detected Background subtracted

o Falling rain causing “motion” in the background. Small drizzle does not cause any problem. We have also tested a sequence taken under a tropical thunderstorm; the results are much poorer, and more works need to be done.

Foreground detected Background subtracted

o Night scene with high image noise, and flickering illumination caused by fluorescent lights. The change in intensity caused by the varying illumination is not a problem as it is entirely captured by the low rank constraint. We have tested our method on other clips taken during dawn and dusk hours, and there the rapidly changing illumination does not cause any problem too.

Foreground detected Background subtracted

o Boat scenes with waves motion in the background. Note that both the large boat in the middle and the small boat in the far distance are detected, demonstrating the scale-invariance of our method.

Foreground detected Background subtracted